Aufbau der Elektronenbeugungsröhre
Eine Elektronenbeugungsröhre ist eine Elektronenstrahlröhre, bei der die Elektronen auf eine Graphiftfolie treffen und anschließend auf einem Fluoreszenzschirm sichtbar gemacht werden.
Experimentelles Ergebnis bei der Elektronenbeugungsröhre
Es ergibt sich das folgende experimentelle Ergebnis:
Auf dem Fluoreszenzschirm sind hellere und dunklere Ringe zu erkennen. Hellere Stellen entstehen dadurch, dass hier mehr Elektronen auf den Fluoreszenzschirm treffen. An dunkleren Stellen treffen weniger Elektronen auf den Schirm. Dies erinnert an frühere Interferenzmuster. Doch ist hier wirklich Interferenz zu sehen?
Ja, es findet Interferenz statt. In der Graphitfolie liegen winzige Kritallfragmente ungeordnet nebeneinander. Treffen Elektronen auf diese Kristallfragmente, so findet Bragg-Reflexion statt. Gemäß der Bragg-Bedingung
\[ n\cdot \lambda = 2\cdot d \cdot \sin(\varphi) \]
entstehen Maxima für die Glanzwinkel $\varphi$. Da wir die Graphitfolie als eine Ansammlung vieler, vieler winziger Kristallfragmente annehmen, darf auch angenommen werden, dass alle Winkel $\varphi$ zwischen der Bewegungsrichtung der Elektronen und der Giterebene des Kristalls tatsächlich existieren. Aufgrund der Rotationssymmetrie der Anordnung entstehen als Interferenzmuster konzentrische Kreise.
Damit haben wir nachgewiesen: der Elektronenstrahl verhält sich wie eine Welle.
Elektronen haben Welleneigenschaften.
Analogie: Gedrehtes Kreuzgitter – Entstehung des ringförmigen Interferenzmusters
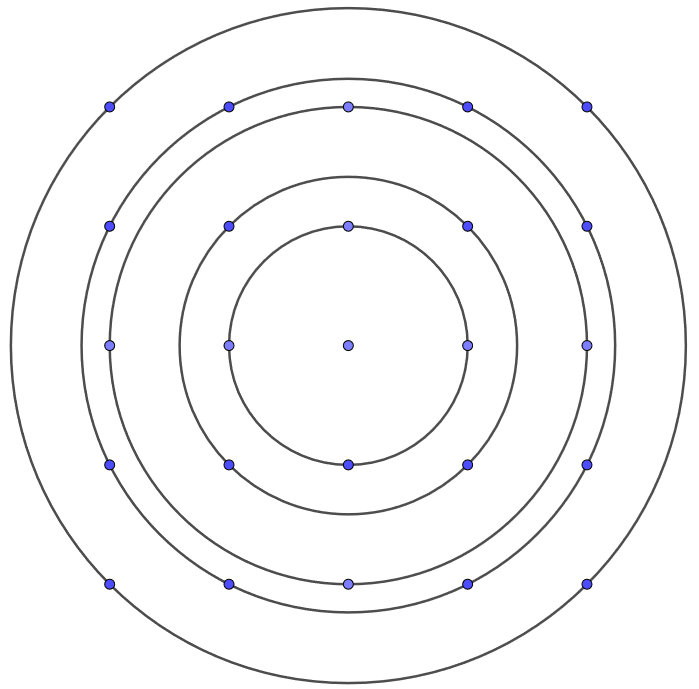
Die bisherige Annahme vieler winziger Kristallfragmente in der Graphitfolie ist ggf. nicht sehr anschaulich. Veranschaulichen kann man das Entstehen des ringförmigen Interferenzmusters mit Hilfe eines sich drehenden Kreuzgitters. Bei diesem Versuch schickt man Laserlicht auf ein sich drehendes Kreuzgitter. Das entstehende Interferenzmuster ist das Muster, das entsteht, wenn das Interferenzmuster des Kreuzgitters ebenfalls gedreht wird.
Wellenlänge der Elektronen und Abhängigkeit von der Spannung
allgemeine Überlegungen
Da wir nachweisen konnten, dass sich die Elektronen wie Wellen verhalten, können wir den Elektronen folglich auch eine Wellenlänge zuordnen. Für Materiewellen wie die betrachtete Elektronenwelle hatte DeBroglie bereits vorab eine Hypothese aufgestellt. Er behauptete:
Die De-Broglie-Wellenlänge wird definiert als $ \lambda = \frac{h}{m\cdot v} $
Dabei ist h das plancksche Wirkungsquantum ($h\approx 6,626\cdot10^-34 \text{ Js}$). Insbesondere war die Wellenlänge von Materiewellen gemäß der Hypothese von DeBroglie also abhängig von der Geschwindigkeit.
Die Geschwindigkeit der Elektronen hängt dabei – wie bei der Elektronenkanone hergeleitet – maßgeblich ab von der Beschleunigungsspannung und es gilt:
\[ v=\sqrt{ \frac{2\cdot e \cdot U_B}{ m_e } } \]
Setzt man dies in dieGleichung für die de-Broglie-Wellenlänge ein, so erhält man für die Wellenlänge: $ \lambda = \frac{h}{\sqrt{ 2\cdot e \cdot U_B \cdot m_e } }$
Beispielrechnung für die Wellenlänge $\lambda$ der Elektronen
Möchte man diesen Zusammenhang experimentell bestätigen, so muss zunächst mit Hilfe der Bragg-Bedingung und der Geometrie der Elektronenbeugungsröhre die Wellenlänge $\lambda$ ermittelt werden.
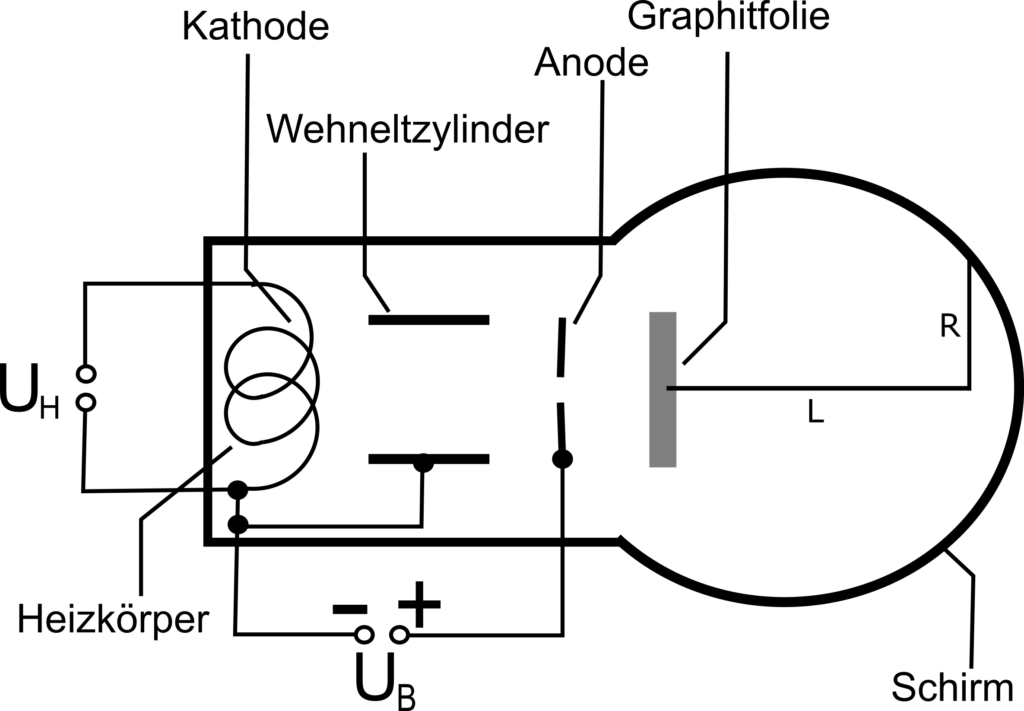
Der Abstand $L$ zwischen Graphitfolie und Fluoreszenzschirm ist in der Regel bekannt. Im Versuch gemessen wird dann der Abstand $R$ eines Maximums (=hellen Rings) vom Mittelpunkt des Schirms. Aus diesen beiden Angaben lässt sich dann der Glanzwinkel $\varphi$ berechnen.
Wir messen für $U_B=3\,000 V$ und $L=13,5 cm$ den Radius der zum ersten Maximum gehört zu $R=1,3 cm$.
Damit ergibt sich für den Glanzwinkel $\varphi$:
\[ \varphi=\arctan\left(\frac{R}{L}\right)= \frac{1,3 cm}{13,5 cm} \approx 5,5^\circ \]
Damit lässt sich nun die Wellenlänge $\lambda$ der Elektronen mit der Bragg-Bedingung berechnen, wobei für den Netzebenenabstand von Graphit $d=0,123 nm$ angenommen werden darf:
\begin{align*} \lambda &= 2d \cdot \sin(\alpha) \\ &= 2\cdot 12,3\cdot10^{-9} m \cdot \sin(5,5^\circ) \\ &\approx 2,358\cdot10^{-11} m\end{align*}
Vergleich der experimentell ermittelten Wellenlänge mit der Hypothese von De-Broglie
Wir vergleichen das Ergebnis mit der Vorhersage durch die de-Broglie-Wellenlänge. Damit ergibt sich ein theoretischer Wert von:
\begin{align*} \lambda &= \frac{h}{\sqrt{ 2\cdot e \cdot U_B \cdot m_e }} \\ &= \frac{h}{\sqrt{ 2\cdot e \cdot 3000 V \cdot m_e}} \\ &\approx 2,239 \cdot 10^{-11 } m \end{align*}
Berechnung der Abweichung:
\[ \frac{2,358\cdot10^{-11} m}{2,239 \cdot 10^{-11 } m} \approx 1,05 \]
Damit weicht unser ermittelter Wert nur um etwa 5% von dem theoretisch zu erwartenden Ergebnis ab.


